【解析几何】准线与焦点
在学习圆锥曲线的过程中,我们必然会遇到诸多有关焦点这个特殊点的题目。比如下面这道:
\[ \text{设}F_1,F_2\text{分别为椭圆}\frac{x^2}{3}+y^2=1\text{的左、右焦点,点}A,B \] \[ \text{在椭圆上,若}\overrightarrow{F_1A}=5\overrightarrow{F_2B},\text{则点A的坐标是}() \]
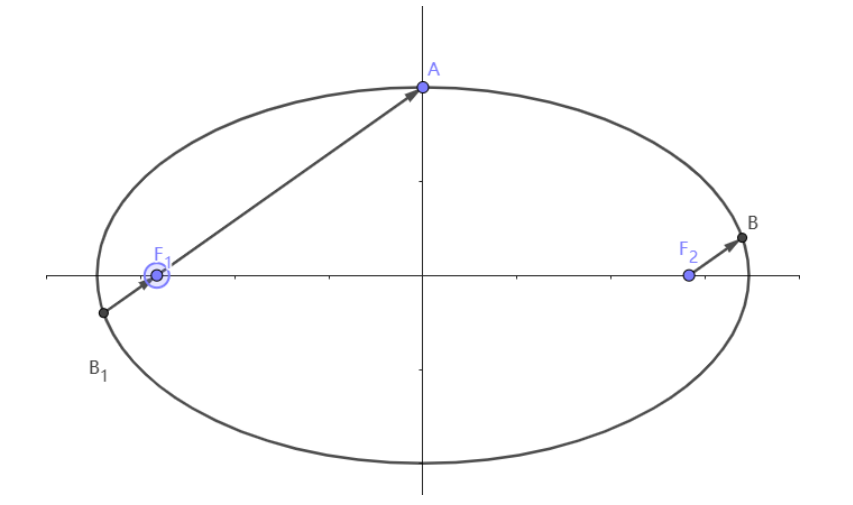
看到这里,很多同学可能就会选择联立求解,如下。
解法一: \[ \text{由于对称性将}\overrightarrow{F_2B}\text{平移到左焦点,设}A(x_1,y_1),B(x_2,y_2) \]
\[ \text{由于直线}AB_1\text{过左焦点,故设}\text{直线}AB_1:x=my-\sqrt{2}. \]
\[ \text{联立} \begin{cases} x=my-\sqrt{2}\\ x^2+3y^2=3 \end{cases} \Longrightarrow(my-\sqrt{2})^2+3y^2=3 \]
\[ \text{则} \begin{cases} y_1=-5y_2\\ y_1+y_2=-\frac{2\sqrt{2}m}{m^2+3}\\ y_1y_2=-\frac{1}{m^2+1} \end{cases} \Rightarrow \]
\[ \left\{ \begin{array}{c} y_1=-\frac{m}{\sqrt{2}(m^2+3)} \\ y_2=\frac{5m}{\sqrt{2}(m^2+3)}\\ \end{array} \right. \Rightarrow \]
\[ \frac{5m^2}{2(m^2+3)}=1 \Rightarrow \]
\[ m=\pm\sqrt{2} \]
\[ \text{所以点}A(0,\pm1) \]
在这里看起来很简单,但计算量还是不小的。
考虑到 \(AB_1\) 是椭圆的焦点弦,我们可以利用焦半径公式。这里就不得不提到圆锥曲线的统一定义了。
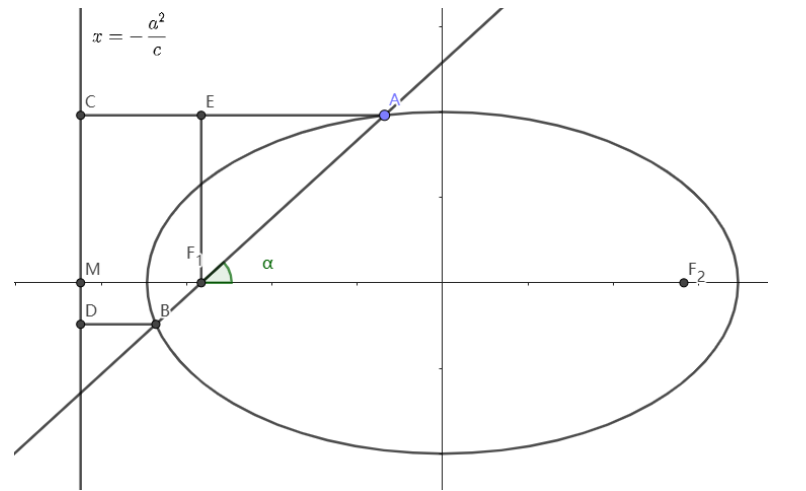
圆锥曲线的统一定义:到定点 \(F\) 的距离与到定直线 \(l\) 的距离(\(F\) 不在 \(l\) 上)的比 \(e\) 是常数的点的轨迹叫作圆锥曲线。 \[ \text{如图,椭圆}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,F_1,F_2\text{为其左右焦点,} \]
\[ \text{直线}l:x=-\frac{a^2}{c}\text{为其左准线,}AC\bot l,\text{则有}\mid AF_1\mid=e\mid AC\mid \]
实际上这也很好“证明”(证明一个“定义”有种儿子生爸爸矛盾了)
\[ \begin{aligned} \text{设点}A(x_0,y_0),\text{则}|AF_1|&=\sqrt{(x_0+c)^2+y_0^2}\\ &=\sqrt{(1-\frac{b^2}{a^2})x_0^2+2cx_0+c^2+b^2}\\ &=\frac{1}{a}\sqrt{c^2x_0^2+2ca^2x_0+a^4}\\ &=\frac{1}{a}\sqrt{(cx_0+a^2)}=a+ex_0 \end{aligned} \]
\[ \text{而}|AC|=x_0+\frac{a^2}{c}=\frac{ex_0+a}{e}=\frac{|AF_1|}{e} \]
一般来说课本内容或一些资料就到此为止了,而我们学习抛物线时会有这么一个结论:
\[ AB\text{是过抛物线}y^2=2px\text{的一条直线,F为抛物线焦点,} \]
\[ \text{A在x轴上方,}\theta\text{为直线AB的倾斜角,则有} \]
\[ |AF|=\frac{p}{1-\cos\theta} \]
\[ |BF|=\frac{p}{1+\cos\theta} \]
\[ |AB|=\frac{2p}{\sin^2\theta} \]
\[ \frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p} \]
那么是不是所有圆锥曲线都有类似性质呢,根据圆锥曲线统一定义我们推断这肯定是存在的。
\[ \text{如上图,对于一个椭圆,设AB的倾斜角为}\alpha,|AF_1|=m,\text{则}|AE|=m\cos\alpha \]
\[ |AC|=\frac{a^2}{c}-c+m\cos\alpha=\frac{am}{c}\Longrightarrow m=\frac{b^2}{a-c\cos\alpha} \]
\[ \text{即}|AF_1|=\frac{b^2}{a-c\cos\alpha} \]
\[ \text{同理可得}|BF_1|=\frac{b^2}{a+c\cos\alpha} \]
\[ |AB|=\frac{2ab}{a^2-c^2\cos^2\alpha},\frac{1}{|AF_1|}+\frac{1}{|BF_1|}=\frac{2a}{b^2} \]
\[ \text{同理,对于双曲线}\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,\text{过其左焦点F的直线AB,有} \]
\[ |AF|=\frac{b^2}{a+c\cos\alpha},|BF|=\frac{b^2}{a-c\cos\alpha},|AB|=\frac{2ab}{a^2-c^2\cos^2\alpha},\frac{1}{|AF_1|}+\frac{1}{|BF_1|}=\frac{2a}{b^2} \]
\[ \text{注意AB交于双曲线左支,所以}|\cos\alpha|\leq\frac{a}{c} \]
利用该结论,再看上面那道题:
\[ \text{设}F_1,F_2\text{分别为椭圆}\frac{x^2}{3}+y^2=1\text{的左、右焦点,点}A,B \]
\[ \text{在椭圆上,若}\overrightarrow{F_1A}=5\overrightarrow{F_2B},\text{则点A的坐标是}() \]
解法二: \[ \begin{aligned} |F_1A|=5|F_1B_1|&\Longrightarrow\frac{1}{\sqrt{3}-\sqrt{2}\cos\theta}=\frac{5}{\sqrt{3}+\sqrt{2}\cos\theta}\\ &\Longrightarrow\cos\theta=\frac{\sqrt{6}}{3}=\frac{c}{a}\\ \end{aligned} \]
\[ \therefore A(0,\pm1) \]
这样计算甚至降到了口算量级,下面我们再来看这样一道题。
\[ \text{设点P为椭圆C:}\frac{x^2}{6}+\frac{y^2}2=1\text{上任意一点,过两焦点}F_1,F_2\text{的弦分别为PA,PB,设} \]
\[ \overrightarrow{PF_1}=\lambda_1\overrightarrow{F_1A},\overrightarrow{PF_2}=\lambda_2\overrightarrow{F_2B},\text{问}\lambda_1+\lambda_2\text{是否是定值,并证明} \]
这里我们直接利用焦点弦结论
\[ \because\frac{1}{|AF_1|}+\frac{1}{|PF_1|}=\frac{1+\lambda_1}{|PF_1|}=\frac{2a}{b^2}=\sqrt{6}\]
\[ \frac{1}{|AF_2|}+\frac{1}{|PF_2|}=\frac{1+\lambda_2}{|PF_2|}=\frac{2a}{b^2}=\sqrt{6} \]
\[ \therefore\sqrt{6}(|PF_1|+|PF_2|)=2+\lambda_1+\lambda_2=2\times6=12 \]
\[ \therefore\lambda_1+\lambda_2=10 \]
几乎是“秒杀”,那么我们来看一道高考题。
\[ \text{已知椭圆}\frac{x^2}{3}+\frac{y^2}{2}=1\text{的左右焦点分别为}F_1,F_2\text{,过点}F_1\text{的直线交椭圆于B,D两点,过点} \]
\[ F_2\text{的直线交椭圆于A,C两点,且}AC\bot BD,\text{垂足为P,求四边形ABCD的面积最小值。} \]
\[ \text{设AC,BD的倾斜角分别为}\alpha,\beta,\text{看到垂直的条件,我们不妨设}\alpha=\beta+\frac{\pi}{2} \]
\[ \text{那么}\cos\alpha=-\sin\beta \]
所以
\[ \begin{aligned} S&=\frac{1}{2}|AC||BD|\\ &=\frac{2a^2b^4}{(a^2-c^2\cos^2\beta)(a^2-c^2\sin^2\beta)}\\ &=\frac{24}{6+\frac{1}{4}sin^22\beta}\\ &\leq\frac{96}{25} \end{aligned} \]
此外利用好点到焦点焦点和点到准线还能处理一些角的问题,如下。
\[ \text{已知抛物线}y^2=2px(p>0)\text{的焦点为F,准线为l} \]
\[ \text{l与x轴交点为M,过点F的直线AB交抛物线于AB两点} \]
\[ A\text{在x轴上方,}∠AMB=\frac{\pi}{3},|AF|=\sqrt{2}+\sqrt{3},\text{试求抛物线方程.} \]
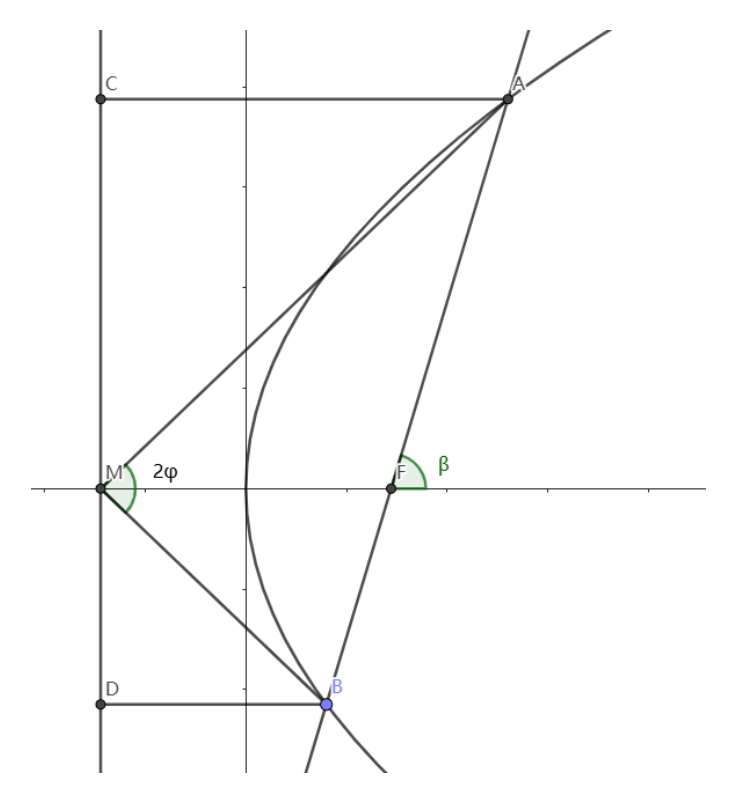
\[ \text{如图设}\angle AMF=\varphi,\text{直线AB的倾斜角为}\beta \]
\[ \text{则有}\sin\beta=\frac{CM}{AF}=\frac{CM}{AC}=\tan\varphi \]
\[ \text{同理}\sin\beta=\tan\angle BMF,\text{所以}\angle AMF=\angle BMF \]
\[ \therefore\sin\beta=\frac{\sqrt{3}}{3},|AF|=\frac{p}{1-\cos\beta}=\sqrt{2}+\sqrt{3} \]
\[ \text{解得:}p=\frac{\sqrt{3}}{3},\text{所以抛物线方程为:}y^2=\frac{2\sqrt{3}}{3}x \]
同样椭圆双曲线也有类似结论,证明也很简单,大家不妨自行尝试推导。
在圆锥曲线部分,有关焦点的问题可以说是俯拾即是,利用上述结论可以迅速解决大部分这类问题,节省大量时间,但同时不要忘记对于基础联立韦达的解法对一般情况进行求解,否则遇到非焦点问题可就是“提笔四顾心茫然”,感谢您的阅读,希望这篇文章能够帮助到你。
