24暑排位2

发表于 2025-08-10 更新于 2025-08-30 分类于 ACM ，题解阅读次数：作者 Pomelorin ， Cool-breeze

Dashboard - SDU 2024暑假排位 Round 2 - Codeforces

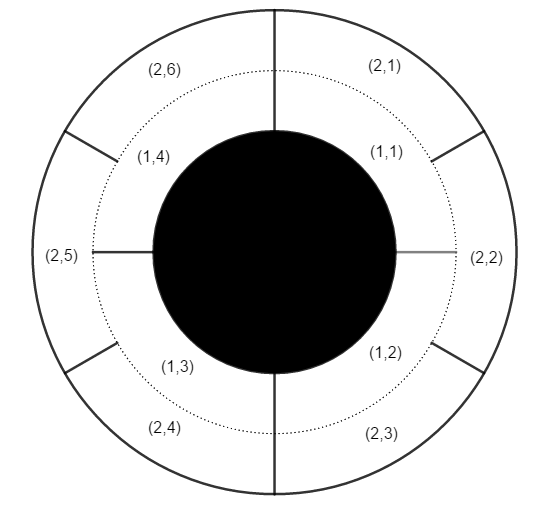
Problem A

一个圆形走廊由两个区域组成。内区域被均匀地分为 \(n\) 个扇区，外区域被均匀地分为 \(m\) 个扇区。每对相同区域（内或外）的扇区之间都有墙壁，但内区域和外区域之间没有墙壁。12 点钟位置总是有一堵墙。

内区域的扇区顺时针方向标记为 \((1,1),(1,2),⋯,(1,n)\)。外区域的扇区同样标记为 \((2,1),(2,2),⋯,(2,m)\)。

有 \(q\) 个询问，是否可以从一个扇区移动到另一个扇区。

\(1≤n,m≤10^{18},1≤q≤10^4\)。

点击查看题解

取 \(n\) 和 \(m\) 的最大公约数 \(g\)。则恰好有 \(g\) 个连通块。一个连通块中，\(n\) 有 \(n/g\) 个扇区，\(m\) 同理。对于每次询问计算两个扇区是否位于同一个连通块即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define PII pair<int,int>

ll n, m, q;

ll gcd(ll a, ll b) {
    return b ? gcd(b, a % b) : a;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll sx, sy, ex, ey, g;
    cin >> n >> m >> q;
    g = gcd(n, m);
    for (ll i = 1; i <= q; i++) {
        ll sty = -1, ety = -1;
        cin >> sx >> sy >> ex >> ey;
        if (sx == 1) {
            sty = (sy - 1) / (n / g);
        } else {
            sty = (sy - 1) / (m / g);
        }
        if (ex == 1) {
            ety = (ey - 1) / (n / g);
        } else {
            ety = (ey - 1) / (m / g);
        }
        if (sty == ety)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

Problem B

一天有 \(h\) 个小时。从第 \(0\) 时（刚好醒来）开始，睡觉 \(n\) 次。第 \(i\) 次睡觉将会在醒来后 \(a_i\) 小时之后准确地再次入睡，睡觉用时正好一天（\(h\) 小时）。

在每天的第 \(l\) 到 \(r\) 小时之间入睡是很棒的。若第 \(i\) 次入睡很棒，称此次睡眠是好的。

为了获取更多好的睡眠，在每次睡觉之前都可以选择：在 \(a_i\) 小时后入睡，或在 \(a_i−1\) 小时后入睡。

求可以获得的好的睡眠次数的最大值。

\(1\le n\le 2000,3\le h\le 2000,0\le l \le r<h,1≤a_i<h\)。

点击查看题解

解法一

可以发现，经过 \(i\) 次睡眠后，只需要知道提前睡了几次就可以算出当前的时间，从而判断睡眠是否很棒。

设 \(f(i,j)\) 代表前 \(i\) 次睡眠提前睡了 \(j\) 次的好的睡眠次数的最大值。限制：\(1\le i\le n, 0\le j\le i\)。

状态转移方程：

\(f(i,j)=\max\{f(i-1,j-1),f(i-1,j)\}+\text{isgood}(i,j)\) 。
\(\text{isgood}(i,j)=[l\le p_i-j\le r\pmod h]\)。
\(p_i\) 表示 \(a_i\) 的前缀和。

时间复杂度 \(O(n^2)\)，适用于 \(n\) 比较小而 \(h\) 比较大的情况。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define PII pair<int,int>

const ll N = 2005;
const ll M = N * N;
ll n, h, l, r, a[N], p[N], f[N][N], ans = 0;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> h >> l >> r;
    for (ll i = 1; i <= n; i++) {
        cin >> a[i];
        p[i] = p[i - 1] + a[i];
    }
    f[0][0] = 0;
    for (ll i = 1; i <= n; i++) {
        for (ll j = 0; j <= i; j++) {
            ll cur = ((p[i] - j) % h + h) % h;
            ll flag = 0;
            if (l <= cur && cur <= r)
                flag = 1;

            if (i > j)
                f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + flag;
            else
                f[i][j] = f[i - 1][j - 1] + flag;
        }
    }
    for (ll i = 0; i <= n; i++)
        ans = max(ans, f[n][i]);
    cout << ans << endl;
    return 0;
}

解法二

可以发现，只用记录睡觉的时间和好的次数，就可以判断睡眠是否很棒。

设 \(f(i,j)\) 代表前 \(i\) 次睡眠后在 \(j\) 小时醒来时，好的睡眠次数的最大值。限制：\(1\le i\le n, 0\le j<h\)。

状态转移方程：

\(f(i,j+a_i) = \max(f(i,j+a_i), f(i-1,j) +\text{isgood}(i,j))\)。
\(f(i,j+a_i-1) = \max(f(i,j+a_i-1), f(i-1,j) +\text{isgood}(i,j))\)。

时间复杂度 \(O(nh)\)。

#include <bits/stdc++.h>
using namespace std;
#define int long long


signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n, h, l, r;
    cin >> n >> h >> l >> r;
    int a[n + 1];
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    int dp[2005] = {};
    int temp[2005] = {};
    dp[0] = 1;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < h; j++) temp[j] = 0;
        for (int j = 0; j < h; j++) {
            if (dp[j] >= 1) {
                int delta = 0, t1 = (j + a[i]) % h, t2 = (j + a[i] - 1) % h;
                if (t1 >= l && t1 <= r)delta = 1;
                temp[t1] = max(temp[t1], dp[j] + delta);
                delta = 0;
                if (t2 >= l && t2 <= r)delta = 1;
                temp[t2] = max(temp[t2], dp[j] + delta);
            }
        }
        swap(dp, temp);
    }
    int ans = 0;
    for (int j = 0; j < h; j++) {
        ans = max(ans, dp[j]);
    }
    cout << ans - 1;
    return 0;
}

Problem C

给定 \(n\) 个点 \(m\) 条边的有向图，边权为 \(1\)。从 \(s\) 出发到达 \(t\)，按照以下路径：\(p_1, p_2, ..., p_k\)，其中 \(p_1=s, p_k=t,p_i\) 两两不同，且保证 \(\forall i\in[1,k-1]\)，边 \((p_i,p_{i+1})\) 存在。

在 \(p_1\)，导航事先生成一条 \(p_1\) 到 \(t\) 的最短路径。对于此路径的每个点 \(p_i\)，如果 \(p_{i+1}\) 恰好沿着导航路径行进，则导航无需重新构建最短路径，否则导航重新构建最短路径。询问导航重新构建最短路径的可能的最小值和最大值。

\(2≤n≤m≤2\times10^5,2≤k≤n\)。

点击查看题解

在反图上跑最短路，同时统计每个点处是否存在多条最短路径在此点分叉的情况即可。

注意，不是统计每个点处的最短路径数量。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define PII pair<ll,ll>

const ll N = 200005;
const ll inf = 1145141919810;
ll n, m, k, p[N], ans1 = 0, ans2 = 0;
ll dis[N], cnt[N], vis[N], in[N];
vector<ll> e[N];

struct CompareMin {
    bool operator()(const PII &a, const PII &b) const {
        return a.second > b.second;
    }
};

priority_queue<PII, vector<PII >, CompareMin> q;
queue<ll> q2;

void add(ll u, ll v) {
    e[u].push_back(v);
}

void dij(ll st) {
    for (ll i = 1; i <= n; i++)
        dis[i] = inf;
    dis[st] = 0;
    q.push({st, 0});
    while (!q.empty()) {
        ll now = q.top().first;
        q.pop();
        if (vis[now])
            continue;
        vis[now] = 1;
        for (auto to: e[now]) {
            if (dis[to] > dis[now] + 1) {
                dis[to] = dis[now] + 1;
                q.push({to, dis[to]});
            }
        }
    }
}

void bfs(ll st) {
    in[st] = 0;
    cnt[st] = 1;
    for (ll i = 1; i <= n; i++) {
        vis[i] = 0;
        for (auto j: e[i]) {
            if (dis[j] == dis[i] + 1)
                in[j]++;
        }
    }
    q2.push(st);
    while (!q2.empty()) {
        ll now = q2.front();
        q2.pop();
        if (vis[now])
            continue;
        vis[now] = 1;
        for (auto to: e[now]) {
            if (dis[to] == dis[now] + 1) {
                cnt[to] += 1;
                in[to]--;
                if (in[to] == 0)
                    q2.push(to);
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    for (ll i = 1; i <= m; i++) {
        ll u, v;
        cin >> u >> v;
        add(v, u);
    }
    cin >> k;
    for (ll i = 1; i <= k; i++)
        cin >> p[i];
    dij(p[k]);
    bfs(p[k]);
    for (int i = 2; i <= k; i++) {
        if (dis[p[i - 1]] - 1 == dis[p[i]]) {
            if (cnt[p[i - 1]] > 1)
                ans2++;
        } else {
            ans1++;
            ans2++;
        }
    }
    cout << ans1 << " " << ans2 << endl;
    return 0;
}

Problem D

\(t\) 组数据，每一组给定一个数组 \(\{a_n\}\)，问是否存在这样一个数组 \(\{b_n\}\)，对于所有 \(i∈[1,n]\)，都存在一组 \(j,k\in[1,n]\)，满足 \(a_i=b_j−b_k\)。

点击查看题解

考虑将数组 \(\{b_n\}\) 构造为 \(0,±a_1,a_1±a_2,a_1±a_2±a_3,⋯,a_1±a_2±a_3±⋯±a_n\)。很显然需要 \(n+1\) 个数，于是只需要其中某个 \(a_i\) 能被节省下来，例如 \(a_n=a_1±a_2±a_3±⋯±a_n-1\)，这样就能节省掉一个数，使得数组 \(\{b_n\}\) 的长度为 \(n\)。

因此，我们只需要判断某个 \(a_i\) 能否表示成一系列的 \(a\) 的和与差的形式，即 \(a_i=a_{j1}±a_{j2}±a_{j3}±⋯±a_{jk}\)。

我们只需要把式子右边的负项移到左边，式子就变成了一堆 \(a\) 加起来等于另一堆 \(a\)。

所以只需要二进制枚举所有可能的和，如果有相同的和，则说明存在这样的式子。

#include <bits/stdc++.h>
using namespace std;
#define int long long
int b[2000005] = {};
// int dp[200005] = {};

void solve() {
    int n;
    cin >> n;
    int a[n + 1];
    memset(b, 0, sizeof(b));
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    for (int i = 0; i <= (1 << n) - 1; i++) {
        int sum1 = 0;
        for (int j = 0; j < n; j++) {
            if ((i & (1 << j)) > 0) {
                sum1 += a[j];
            }
        }
        b[sum1 + 1000000]++;
        if (b[sum1 + 1000000] > 1) {
            cout << "YES";
            return;
        }
        cout << "NO";
    }

    signed main() {
        ios::sync_with_stdio(false);
        cin.tie(0);
        cout.tie(0);
        int t;
        cin >> t;
        while (t--) {
            solve();
            cout << endl;
        }
        return 0;
    }
}

时间复杂度 \(O(2^n)\)。

Problem E

你有一个长度为 \(n\) 的字符串，字符集为小写英文字母 \(C\)。你可以选择它的任意一个子序列。对于一个长度为 \(m\) 的子序列，选出它的花费是 \(n−m\)，也就是你需要删掉的字符数量。你的任务是选出来 \(k\) 个不同的子序列，使得总花费最小。输出这个最小花费。如果选不出 \(k\) 个，输出 \(−1\)。

\(1≤n≤100,1≤k≤10^{12}\)。

点击查看题解

设 \(f(i,j,k)\) 表示考虑前 \(i\) 个字符，长度为 \(j\) 且最后一个字母为 \(k\) 的不同字符串数量。

设第 \(i\) 个字符为 \(a_i\)。状态转移方程： \[ \forall l\in C,l\not=a_i, f(i,j,l)=f(i-1,j,l) \]

\[ f(i,j,a_i)=\sum_{k\in C} f(i-1,j-1,k) \]

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define PII pair<ll,ll>

const ll N = 105, M = 30;
ll n, k, f[N][N][M], a[N], ans = 0, cnt = 0;
string s;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> k >> s;
    s = ' ' + s;
    for (ll i = 1; i <= n; i++)
        a[i] = s[i] - 'a' + 1;

    for (ll i = 1; i <= n; i++) {
        for (ll j = 0; j <= i; j++) {
            if (j == 0) {
                f[i][j][0] = 1;
            }
            if (j == 1) {
                f[i][j][a[i]] = 1; //y
                for (ll k = 1; k <= 26; k++) {
                    if (k == a[i])
                        continue;
                    f[i][j][k] = f[i - 1][j][k]; //n
                }
            }
            if (j >= 2) {
                for (ll k = 1; k <= 26; k++) {
                    f[i][j][a[i]] += f[i - 1][j - 1][k]; //y
                    if (k == a[i])
                        continue;
                    f[i][j][k] = f[i - 1][j][k]; //n
                }
            }
        }
    }
    for (ll i = n; i >= 0; i--) {
        for (ll j = 1; j <= 26; j++) {
            f[n][i][0] += f[n][i][j];
        }
        if (cnt + f[n][i][0] >= k) {
            ans += (k - cnt) * (n - i);
            cout << ans << endl;
            return 0;
        }
        cnt += f[n][i][0];
        ans += f[n][i][0] * (n - i);
    }
    cout << "-1" << endl;
    return 0;
}