线段树

发表于 分类于 ， 阅读次数：

简介

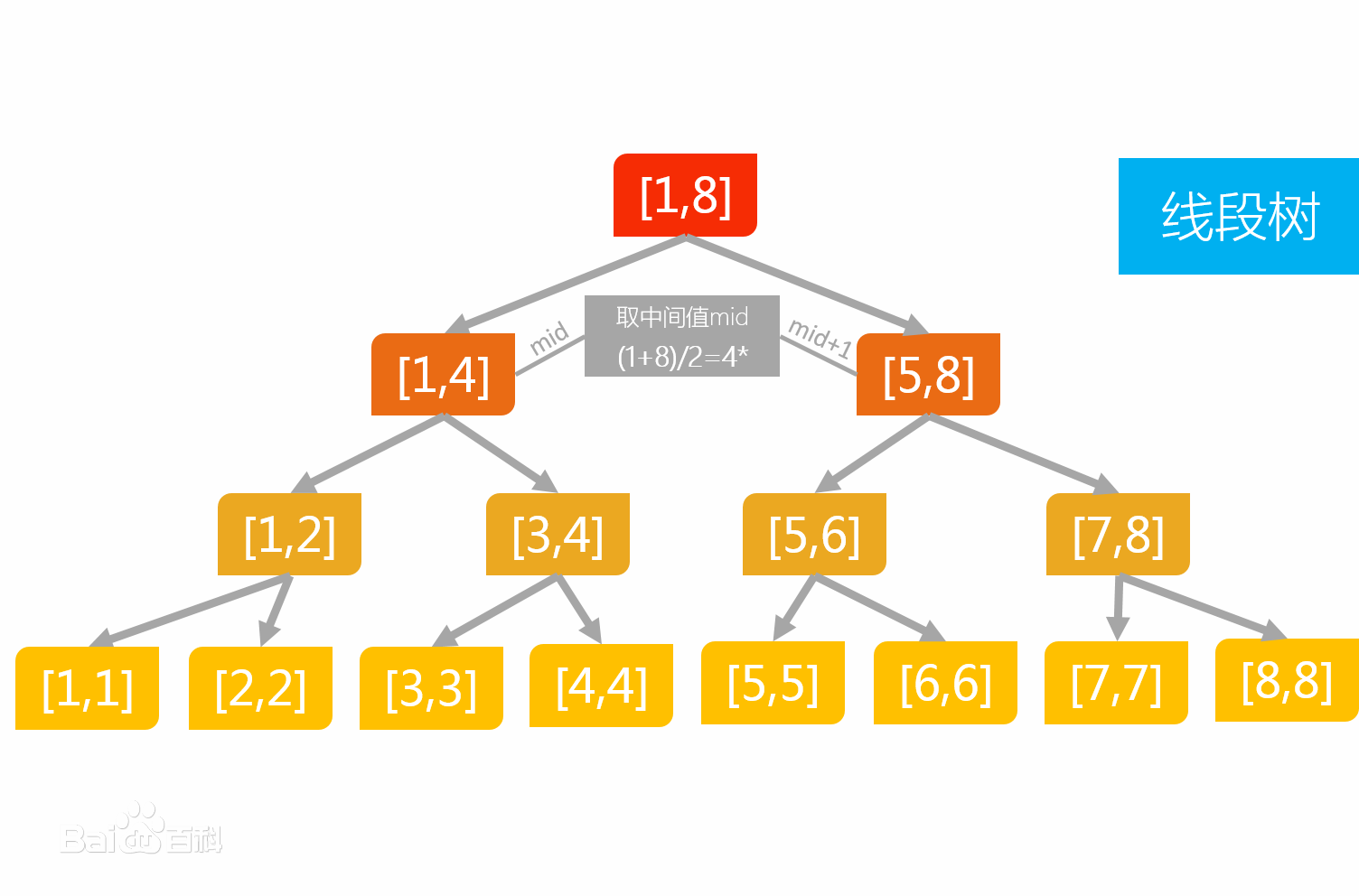
线段树，是用来存放给定区间内对应信息的一种数据结构，是一种二叉搜索树。可用来处理数组相应的单点、区间修改操作，也可以进行区间最值、区间和等的查询。

线段树是一种二叉搜索树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。子节点向父节点传递信息，而父节点存储的信息则是子节点信息的整合。

用 Node[l,r] 表示线段树表示区间 [l,r] 的节点。其儿子就是 Node[l,(l+r)/2] Node[(l+r)/2+1,r]。当 \(l\) 与 \(r\) 相等时为叶子，停止，这样尽量等分下去的树形结构。（值）

存储可同样使用数组，下标表示编号。对于编号为 p 的节点，p*2 即为左儿子，p*2+1 即为右儿子。（键）

线段树的时间复杂度可达 log 级别。而未优化的空间复杂度为 4N 级别，因此有时需要动态开点让空间压缩。

操作（Part 1）

1
2
3
4
#define ll long long
#define lson (root*2)
#define rson ((root*2)+1)
#define mid ((l+r)/2)

代码以单点/区间修改，区间求和为例。

建树

建树直接按照上述规则递归即可。相当于是在 DFS 线段树，边 DFS 边建立。

1
2
3
4
5
6
7
8
void build(ll root,ll l,ll r,ll d[])
{
	if(l==r){t[root]=d[l];return;}
	build(lson,l,mid,d);
	build(rson,mid+1,r,d);
	t[root]=t[lson]+t[rson]; //pushup
	return;
}

区间查询

怎么查询信息呢？既然这个要查询的区间被分为了 log n 个节点，那么找到这 log n 个节点，即可递归进行查找。

1
2
3
4
5
6
7
8
ll query(ll root,ll l,ll r,ll x,ll y)
{
	if(x<=l&&y>=r) return t[root];
	ll ansl=0,ansr=0;
	if(x<=mid) ansl=query(lson,l,mid,x,y);
	if(y>mid) ansr=query(rson,mid+1,r,x,y);
	return ansl+ansr;
}

单点修改

单点修改就是指只修改线段树的某个叶子节点的值，修改叶子节点会对其父节点的值产生影响，因此修改子节点后，要回溯更新其父节点的值。

1
2
3
4
5
6
7
void update(ll root,ll l,ll r,ll pos,ll data)
{
	if(l==r) {t[root]+=data;return;}
	if(pos<=mid) update(lson,l,mid,pos,data);
	if(pos>mid) update(rson,mid+1,r,pos,data);
	t[root]=t[lson]+t[rson];
}

线段树三问

处理较难的线段树问题的常用套路，以单点修改（加某一个值）、区间查询为例：

  1. 维护哪些信息？区间和。
  2. 如何合并区间信息？直接相加。
  3. 如何修改信息？直接相加。

例题（Part 1）

某经典问题

给一个长为 N 的数列，有 M 次操作，每次操作时以下三种之一：

  • 修改数列中的一个数
  • 求数列中某连续一段所有数的两两乘积的和（mod 1e9+7）
  • 求数列中某连续一段所有相邻两数乘积的和（mod 1e9+7）

N 和 M 均为 1e5。

解答

假设 x 节点的儿子为 y 和 z。

x 相邻两数乘积的和为：y 相邻两数乘积的和 + z 相邻两数乘积的和 + y 最右边的数 * z 最左边的数。

x 任意两数乘积的和为：y 任意两数乘积的和 + z 任意两数乘积的和 + y 的和 * z 的和。

然后直接维护即可。

  1. 维护哪些信息？相邻两数乘积的和，任意两数乘积的和，最左边的数，最右边的数，区间和。

    我们可以发现，为了求解，往往需要额外维护其他信息。

  2. 如何合并区间信息？

    • 相邻两数乘积的和、任意两数乘积的和，如上所述。
    • x 最左边的数为 y 最左边的数，x 最右边的数为 z 最右边的数。
    • x 的和为 y 的和加 z 的和。

  3. 如何修改信息？单点修改叶子节点，之后向上传递更新。

P4513 小白逛公园

1e5 长度序列，单点修改，询问区间最大子段和。最大子段和指的是找出一个可以是空的子区间，和最大。

解答

可以想到，对于节点 x 的答案，答案要么是 y 或 z 本身的答案，要么跨越 y 和 z。

  1. 维护哪些信息？区间最大子段和，左起最大前缀，右起最大后缀，区间和。

  2. 如何合并区间信息？

    区间最大子段和： y 区间最大子段和，z 区间最大子段和，y 右起最大后缀 + z 左起最大前缀 三者取最大值。

    左起最大前缀：y 左起最大前缀，y 区间和 + z 左起最大前缀 两者取最大值。右起最大后缀同理。

    区间和：y 区间和加 z 区间和。

  3. 如何修改信息？单点修改叶子节点，之后向上传递更新。

课后习题

操作（Part 2）

涉及到区间修改的问题没法快速的直接进行修改。

每次线段树操作会涉及到 log 个线段树的节点，而且一个点被访问当且仅当其父亲节点被访问过，所以我们可以用“懒惰”的思想来维护。

懒惰标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。

这个最重要的思想就是，我们每次操作只会访问到少数线段树上的节点，那对于没有被访问到的节点，比如这些节点子树内部的节点，我们不需要维护其经过区间修改后的值，只需要保证这些节点被访问到的时候是正确的就行。

下放标记

以区间加、求区间和举例子：

我们在每个节点上维护一个懒惰标记，代表这个节点被加了多少值，但是其儿子因暂时未访问而暂未修改。

查询的时候对于每个经过的节点，下放标记到其儿子：首先对儿子区间加 tag（代表标记对区间信息的影响），之后将 tag 传递给儿子（代表多个标记的合并）。

这样我们查询的时候还是查询 log 个节点，与之前的不同的是，每个节点有可能被整体加了一个值。

1
2
3
4
5
6
7
8
9
10
void pushdown(ll root,ll l,ll r)
{
	ll tag=t[root].tag;
	if(t[root].tag==0) return;
	t[lson].data+=tag*(mid-l+1);
	t[rson].data+=tag*(r-mid);
	t[lson].tag+=tag;t[rson].tag+=tag;
	t[root].tag=0;
	return;
}

区间修改

我们考虑一下引入懒标记后，线段树需要支持什么。

  1. 两个区间维护的信息的合并：这个是最基本的，我们维护出了两个区间 [l,mid],[mid+1,r] 的信息要能够快速合并出 [l,r] 的信息，否则这个问题线段树不能解决。
  2. 一个线段树节点上多个标记的合并：标记之间要可以快速合并，比如区间加标记，区间 +a 和 +b 合并后变成区间 +(a+b)；区间修改标记，区间先修改为 a，后修改为 b，合并后变成区间修改为 b。
  3. 标记对区间信息的影响：这个一般是最麻烦的一步。我们维护出了线段树上一个的信息，要支持这个节点被修改后，这个信息能快速计算出来。比如区间加区间和，当前线段树节点区间和为 a，区间长度为 len，我们加上 b，则区间和变为 (a+len*b)；区间修改区间和，当前线段树节点区间和为 a，区间长度为 len，我们加上 b，则区间和变为 len*b。

区间查询、区间修改时，在下一步访问儿子之前，必须要进行 pushdown 操作，以免儿子未更新导致错误。

1
2
3
4
5
6
7
8
9
10
11
12
13
void update(ll root,ll l,ll r,ll x,ll y,ll data)
{
	if(x<=l&&y>=r)
	{
		t[root].data+=data*(r-l+1);
		t[root].tag+=data;
		return;
	}
	pushdown(root,l,r);
	if(x<=mid) update(lson,l,mid,x,y,data);
	if(y>mid) update(rson,mid+1,r,x,y,data);
	t[root].data=t[lson].data+t[rson].data;
}

总结

线段树可以简单地抽象为一个有以下功能的数据结构：对一个范围进行某种可以快速维护的操作，查询一个范围内的某个可以合并的信息。

通俗来说就是：

  • 单点修改，查询区间的某个信息；
  • 区间修改，查询单点的某个信息；
  • 区间修改，查询区间的某个信息。

这三个都是线段树的功能。

线段树六问

处理较难的线段树问题的常用套路，以区间加、区间查询为例：

  1. 维护哪些信息？区间和。
  2. 维护哪些标记？区间加标记。
  3. 如何合并区间信息？直接相加。
  4. 如何快速修改区间信息与标记信息？区间信息加上 增量乘区间长度，标记信息加上增量。
  5. 如何合并标记？直接相加。
  6. 如何利用标记修改信息？加上 标记乘区间长度。

例题（Part 2）

P3372 【模板】线段树 1

区间加、区间求和模板题。

P3373 【模板】线段树 2

  • 将某区间每一个数乘上 x；
  • 将某区间每一个数加上 x；
  • 求出某区间每一个数的和。
解答

我们发现一个标记是不能够解决问题的，那就上两个，分别表示乘法的 mul 和加法的 add。紧接着想到两个标记并非相互独立，需要人为规定标记修改信息。

例如我们规定：先 mul 修改信息，之后 add 修改信息，即 d=d*mul+add*len。

  • 如果一个节点被加上了 x，则 add+=x，mul 不变。
  • 如果一个节点被乘上了 x，则 add*=x，mul*=x。因为如果在此之前已经有 add 标记，说明这个节点应当加 add，之后的乘法对 add 也有影响。由于 add 暂未真的加在节点上（懒标记），add 也需要体现乘法的影响。
  1. 维护哪些信息？区间和 d。
  2. 维护哪些标记？add 与 mul。
  3. 如何合并区间信息？直接相加。
  4. 如何快速修改区间信息与标记信息？对于加法，加上 x*len；对于乘法，直接乘 x。标记信息修改如上。
  5. 如何合并标记？[] 表示子节点的标记。[add]=[add]*mul+add, [mul]*=mul。
  6. 如何利用标记修改信息？d=d*mul+add*len。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
struct SGT
{
	#define lson (root*2)
	#define rson ((root*2)+1)
	#define mid ((l+r)/2)
	struct node{ll d,atag,mtag;}t[N*4];
	void pushup(ll root)
	{
		t[root].d=(t[lson].d+t[rson].d)%p;
	}
	void pushdown(ll root,ll l,ll r)
	{
		ll mtag=t[root].mtag%p;
		ll atag=t[root].atag%p;
		t[lson].mtag=t[lson].mtag*mtag%p;
		t[rson].mtag=t[rson].mtag*mtag%p;
		t[lson].d=t[lson].d*mtag%p;
		t[rson].d=t[rson].d*mtag%p;
		t[lson].atag=(t[lson].atag*mtag+atag)%p;
		t[rson].atag=(t[rson].atag*mtag+atag)%p;
		t[lson].d=(t[lson].d+atag*(mid-l+1))%p;
		t[rson].d=(t[rson].d+atag*(r-mid))%p;
		t[root].atag=0; t[root].mtag=1;
	}
	void build(ll root,ll l,ll r)
	{
		t[root].mtag=1;
		t[root].atag=0;
		if(l==r)
		{
			t[root].d=a[l]%p;
			return;
		}
		build(lson,l,mid);
		build(rson,mid+1,r);
		pushup(root);
	}
	ll query(ll root,ll l,ll r,ll x,ll y)
	{
		if(x<=l&&r<=y) return t[root].d%p;
		ll al=0,ar=0;
		pushdown(root,l,r);
		if(x<=mid) al=query(lson,l,mid,x,y);
		if(y>mid) ar=query(rson,mid+1,r,x,y);
		return (al+ar)%p;
	}
	void aupdate(ll root,ll l,ll r,ll x,ll y,ll d)
	{
		if(x<=l&&r<=y)
		{
			t[root].d=(t[root].d+d*(r-l+1))%p;
			t[root].atag=(t[root].atag+d)%p;
			return;
		}
		pushdown(root,l,r);
		if(x<=mid) aupdate(lson,l,mid,x,y,d);
		if(y>mid) aupdate(rson,mid+1,r,x,y,d);
		pushup(root);
	}
	void mupdate(ll root,ll l,ll r,ll x,ll y,ll d)
	{
		if(x<=l&&r<=y)
		{
			t[root].d=t[root].d*d%p;
			t[root].atag=t[root].atag*d%p;
			t[root].mtag=t[root].mtag*d%p;
			return;
		}
		pushdown(root,l,r);
		if(x<=mid) mupdate(lson,l,mid,x,y,d);
		if(y>mid) mupdate(rson,mid+1,r,x,y,d);
		pushup(root);
	}
}tree;

课后习题

权值线段树（Part 3）

根据维护数值分类：值域线段树、权值线段树。之前我们讲的都是值域线段树，接下来我们讲权值线段树。

权值线段树每个节点存储的是某个值域区间内元素出现的次数（可理解为 multiset），常用于如查询第 k 小/大值、区间频次等。相比平衡树，权值线段树实现简单、常数小，但在值域较大时需配合离散化或动态开点降低空间消耗。

如果我们讲之前单点加、区间求和的值域线段树理解为权值线段树，则变为：

  • 向集合内添加 x 个整数 d（单点 d 加 x）；
  • 求 [l,r] 内出现了多少整数（区间 [l,r] 求和）。

动态开点线段树

前面讲到堆式储存的情况下，需要给线段树开 4n 大小的数组。

为了节省空间，我们可以不一次性建好树，而是在最初只建立一个根结点代表整个区间。当我们需要访问某个子区间时，才建立代表这个区间的子结点。

这样我们不再使用 p*2 代表左儿子、p*2+1 代表右儿子，而是用 ls 和 rs 记录儿子的编号。总之，动态开点线段树的核心思想就是：结点只有在有需要的时候才被创建。

一般来说，动态开点线段树不需要 build 函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
ll cnt=0;
struct SGT
{
	struct node{int lson,rson,data;}t[N];
	#define lson t[root].lson
	#define rson t[root].rson
	#define mid ((l+r)/2)
	ll update(ll root,ll l,ll r,ll pos,ll data)
	{
		if(root==0) root=++cnt;//开辟新节点
		if(l==r)
		{
			t[root].data+=data;
			return root;
		}
		if(pos<=mid) lson=update(lson,l,mid,pos,data);
		else rson=update(rson,mid+1,r,pos,data);
		t[root].data=t[lson].data+t[rson].data;
		return root;//返回地址
	}
	ll query(ll root,ll l,ll r,ll x,ll y)
	{
		ll ret=0;
		if(root==0) return 0;
		if(x<=l&&r<=y) return t[root].data;
		if(x<=mid) ret+=query(lson,l,mid,x,y);
		if(y>=mid+1) ret+=query(rson,mid+1,r,x,y);
		return ret;
	}
}Tree;

例题（Part 3）

P1908 逆序对

求一个数列的逆序对个数。

解答

逆序对个数为每个元素前面比此元素大的个数之和。

维护一棵权值动态开点线段树，其根节点管辖范围为 \(1\) 至 \(10^9\)。

在 \(10^9\) 的管理区间上，找到一点 \(i\)，不超过 \(30\) 次，会经过不超过 \(30\) 个节点，这些节点是我们实现对 \(i\) 的操作所必须的，所以如果有对 \(i\) 的操作，我们就动态开辟这些经过的节点。

按照定义，从 \(1\) 至 \(n\)，先查询 \([a_i,10^9]\) 区间和（比 \(a_i\) 大的数的个数），累加到 \(ans\)，再向线段树中插入数字。

或者离散化使用普通权值线段树。

课后习题